!Дерево отрезков

Дерево отрезков(англ. Segment tree) - структура данных, позволяющая насчитывать любую ассоциативную функцию на любом отрезке массива за $O({\log }_{2}n)$ с изменениями за $O({\log }_{2}n)$. Также поддерживает персистентность и изменения на отрезке за $O({\log }_{2}n)$.

Описание базовой версии алгоритма

На самом деле удобнее хранить ответы не на отрезках, а на полуинтервалах. Пусть у нас будет полуинтревал, содержащий ответ на всем массиве, он будет корнем нашего дерева. Для каждой вершины ее правый сын будет содержать ответ на правой половине его полуинтервала, а левый сын на левой, если это записать в формуле, то если вершина содержит ответ на $[l;r)$, то ее левый сын содержит ответ на $\left[l;\frac{l+r}{2}\right)$, а правый на $\left[\frac{l+r}{2};r\right)$. Высота нашего дерева получится ${\log }_{2}n$, потому что на каждом следующем уровне длина отрезка уменьшается в 2 раза. Теперь поймем, почему ответ на отрезке работает быстро. Чтобы его считать мы запускаемся от корня и если текущий отрезок полностью лежит в искомом, то мы считаем ответ от него и выходим, если он полностью не лежит, то просто выходим, а в последнем случаем запускаемся от его сыновей. На каждой высоте будет посещено не более 4 вершин, ведь не более 2 из них затронуты не полностью - самая левая и самая правая, остальные полностью содержат запрашиваемый отрезок, тогда мы зайдем в не более 2 отрезков из них, ведь остальные разобьются на пары, в каждой из которых у вершин общий предок, и мы возьмем его, не заходя в потомков. Следовательно, асимптотика работы равна высоте дерева, то есть $O({\log }_{2}n)$. Изменение в одном элементе также работает за $O({\log }_{2}n)$, и чтобы его совершить мы стартуем из вершины, содержащей только этот элемент, меняем ответ и переходим в предка. Таким образом мы сделаем изменение всех отрезков, содержащих конкретный элемент, и так как их ровно ${\log }_{2}n$, то и работать изменение элемента будет за $O({\log }_{2}n)$.

Построение

Существует 2 разновидности ДО - ДО снизу и ДО сверху. Я распишу оба варианта и для каждого приведу только одну реализацию, этого вполне достаточно чтобы решить все задачи на ДО, которые могут вам встретиться. Различаются эти 2 ДО только построением и реализацией запроса, ДО снизу сначала строит листы дерева, а потом итеративно высчитывает ответ для их предков, ДО сверху напротив запускается от корня и рекурсивно строит дерево целиком. Запросы происходят также. Для наипростейшей задачи на ДО лучше подойдет построение снизу, ведь оно быстрее из-за того что работает итеративно, а не рекурсивно, и реализовано с помощью битовых операций, пишется проще и быстрее, ну а если вам нужен большой функционал, например неявное ДО или персистентное ДО, то вам однозначно лучше писать это с помощью ДО сверху на указателях.

Дерево отрезков сверху

Алгоритм работы этого варианта дерева отрезков был описан в предыдущем пункте, можно писать его как на массиве, так и на указателях, указатели в c++ очень медленные, а также занимают много памяти, поэтому рекомендуется использовать массив с кастомной структурой вершины, которая может иметь ссылки на потомков, а также значения в самой вершине и значение для массовых операций.

Код ДО сверху

Структура вершины:

struct st_node {
	long long s_l = -1, s_r = -1, x = 0, l, r, num, pr = -1;
	st_node(long long _x, long long _l, long long _num) : x(_x), l(_l), num(_num) {
		r = l + 1;
	}
	st_node(st_node *_s_l, st_node *_s_r, long long _num,
	long long (*f)(long long, long long) = func) : num(_num) {
		_s_l->pr = num;
		_s_r->pr = num;
		s_l = _s_l->num;
		s_r = _s_r->num;
		x = f(_s_l->x, _s_r->x);
		l = _s_l->l;
		r = _s_r->r;
	}
	st_node() {}
};

Построение дерева:

vector<st_node *> st;
vector<long long> arr;
st_node *root = nullptr;
 
st_node *build_tree(long long l, long long r) {
	if (l + 1 == r) {
		st.push_back(new st_node(arr[l], l, st.size()));
		return st[st.size() - 1];
	}
	long long m = (r + l) / 2;
	auto res1 = build_tree(l, m), res2 = build_tree(m, r);
	long long num = st.size();
	st.push_back(new st_node(res1, res2, num, func));
	return st[num];
}
 
int main() {
	long long n;
	cin >> n;
	arr.resize(n);
	for (long long i = 0; i < n; i++) {
		cin >> arr[i];
	}
	root = build_tree(0, n);
}

Подсчет ответа:

long long get_ans(long long l, long long r,
long long (*f)(long long, long long) = func, st_node *v = root) {
	if (v->l >= l && v->r <= r) {
		return v->x;
	}
	if (v->l >= r || v->r <= l) {
		return 0;
	}
	return f(get_ans(l, r, f, st[v->s_l]), get_ans(l, r, f, st[v->s_r]));
}

Дерево отрезков снизу

Пишется на массиве и является самой легкой и быстрой реализацией ДО. Ответ на всем отрезке будет лежать в нулевой ячейке, а также для каждого отрезка, лежащего в ячейке i, левая часть его отрезка лежит в ячейке $2i+1$, а левая в $2i+2$, так и задается весь массив. Лучше в реализации сначала подсчитать максимальный размер получившегося ДО и округлить его до ближайшей большей степени 2 - maxn и завести массив размера $2maxn-1$, в котором последние maxn вершин будут листьями. После их заполнения стартовыми значениями можно итеративно насчитать ответ и во всех предыдущих вершинах. Тогда чтобы получить ответ на $[l,r]$ мы ставим указатели на листы, соответствующие данным вершинам и выполняем этот алгоритм:

1. Проверяем является ли вершина на которую указывает левый указатель правым сыном? Для этого просто проверяем четный ли у нее номер. Если да, то надо через нее обновить ответ и сдвинуть ее вправо.
2. Проверяем является ли вершина на которую указывает правый указатель левым сыном? Для этого просто проверяем нечетная ли у нее номер. Если да, то надо через нее обновить ответ и сдвинуть ее влево.
3. Если указатели совпали, то обновляем ответ и выходим, иначе поднимаемся из каждого указателя в предка и если они совпали, то обновляем ответ и выходим, иначе повторяем алгоритм. Это работает очень быстро из-за простоты деления на 2 для компилятора и работы с массивом, а не с указателями, но персистентность, массовые операции и неявность добавить сюда очень сложно, поэтому их лучше писать с помощью ДО сверху.

Код ДО снизу на массиве

Вы можете использовать функцию, которая и будет использоваться везде далее:

long long func(long long x, long long y) {
  return x + y;
}

Построение(для улучшения производительности используйте intы и массив вместо вектора):

long long n;
cin >> n;
long long maxsz = 1;
while (maxsz < n * 2) {
  maxsz *= 2;
}
vector<long long> st(maxsz - 1);
long long beg = 1 + (maxsz - 4) / 2;
for (long long i = 0; i < n; i++) {
  cin >> st[beg++];
}
for (long long i = (maxsz - 4) / 2; i > -1; i--) {
  st[i] = func(st[i * 2 + 1], st[i * 2 + 2]);
}

Подсчет ответа:

long long get_ans(long long l, long long r, long long (*f)(long long, long long) = func) {
  l += 1 + (st.size() - 3) / 2;
  r += 1 + (st.size() - 3) / 2;
  long long ans = 0;
  while (l + 1 < r) {
  	if (l % 2 == 0) {
  		ans = f(ans, st[l]);
  		l++;
  	}
  	if (r % 2 == 0) {
  		ans = f(ans, st[r - 1]);
  		r--;
  	}
  	l--;
  	r--;
  	l /= 2;
  	r /= 2;
  }
  if (l + 1 == r) {
  	ans = f(ans, st[l]);
  }
  return ans;
}

Отложенные массовые операции

Иногда на олимпиадах нас просят делать изменения не только в одной вершине, но и сразу на целом отрезке, что займет $O(n{\log }_{2}n)$ на запрос, если использовать прошлый способ. Но уже можем считать ответ на отрезке за $O({\log }_{2}n)$, можно попытаться использовать этот способ и для изменений. Очевидно, что честно менять все элементы при запросе мы точно не можем, это займет $O({\log }_{2}n)$, но нам это и не нужно, мы хотим, чтобы при запросе ответа все значения, до которых мы дошли, были актуальны, тогда мы можем просто зафиксировать изменение на самом запросе изменения, а насчитать его для нужных вершин только тогда, когда нам они понадобятся для подсчета ответа. Это и называется отложенными операциями, мы заводим дополнительную переменную для каждой вершины, в которой и запишем изменение, которое должны будем совершить с этим отрезком, а также функцию push, которую всегда запускаем перед работой с вершиной, она обновляет ответ в ней и проталкивает запись дальше в потомков.

Код для ДО сверху

Для того чтобы избежать ошибки, которую я описал в примечании, я разделил стандартную реализацию push на 2 функции: сам push и update, который на самом деле делает всю грязную работу за push и обновляет значение в вершине и проталкивает все значения дальше:

void update(st_node *v) {
if (v->upd == -1) {
	return;
}
	v->x = v->upd * (v->r - v->l);
	if (v->s_l != -1) {
	st[v->s_l]->upd = v->upd;
	st[v->s_r]->upd = v->upd;
	}
	v->upd = -1;
}
 
void push(st_node *v, long long (*f)(long long, long long) = func) {
	if (v->s_l == -1) {
		update(v);
		return;
	}
	update(v);
	update(st[v->s_l]);
	update(st[v->s_r]);
	v->x = f(st[v->s_l]->x, st[v->s_r]->x);
}

Вот код для обновления на отрезке:

void update(long long l, long long r, long long x,
long long (*f)(long long, long long) = func, st_node *v = root) {
	push(v);
	if (v->l >= l && v->r <= r) {
		v->upd = x;
		push(v);
		return;
	}
	if (v->l >= r || v->r <= l) {
		return;
	}
	update(l, r, x, f, st[v->s_l]);
	update(l, r, x, f, st[v->s_r]);
	push(v);
}

Примечание

Чтобы это работало быстро мы должны иметь изменение, для которого понятно, насколько оно влияет на тот или иной отрезок и не требует честного высчитывания этого у потомков, иначе это также будет работать за $O({\log }_{2}n)$. Кроме этого, массовые операции будут работать, только если новая операция полностью перекрывает старую на том же отрезке, например приравнивание на отрезке, если же результат прошлой операции важен для текущей, то массовые операции будут работать неправильно. Также после записи в вершине мы должны уметь понимать, что нужно записать в сыновьях, и ни в коем случае не запускать push от них. В целом, если ваш push запускается от потомков и вы математически не доказали, что таких запусков будет мало и все работает быстро, то ваш push работает неправильно.

Неявное дерево отрезков

В некоторых задачах очень большие ограничения и все, кроме построения дерева у нас работает за $O({\log }_{2}n)$ и поэтому нас устраивает. Чтобы избавиться от построения, можно представить, что дерево уже существует и создавать его в течении последующих запросов, для этого можно улучшить push, в котором мы будем дополнительно проверять существование обоих сыновей вершины и создавать их, если они отсутствуют. Но если все запросы вам уже известны, то проще сжать координаты и не писать неявное ДО.

Код для ДО сверху

Реализация этой вариации ничем особо не отличается, просто удалите build_tree и вместо него просто создайте корень, а при переходе в потомка проверьте, существует ли он, и если нет, то создайте его и заполните все его поля.

Персистентное дерево отрезков

Дерево отрезков можно сделать персистентным, для этого достаточно вспомнить, что при каждом изменении элемента ответ меняется только в ${\log }_{2}n$ вершинах - его предках. Тогда, чтобы сделать дерево персистентным, нам нужно при каждом изменении можно рекурсивно запускаться от листа измененного элемента, создавать его копию, менять в ней ответ и запускаться от предка. Так мы поднимемся до корня, в вершинах мы будем ссылаться на нового сына, если он поменялся, или на старого, если изменений в нем не было. В конце мы получим новый корень, от которого можно будет запуститься, чтобы получить определенную версию дерева.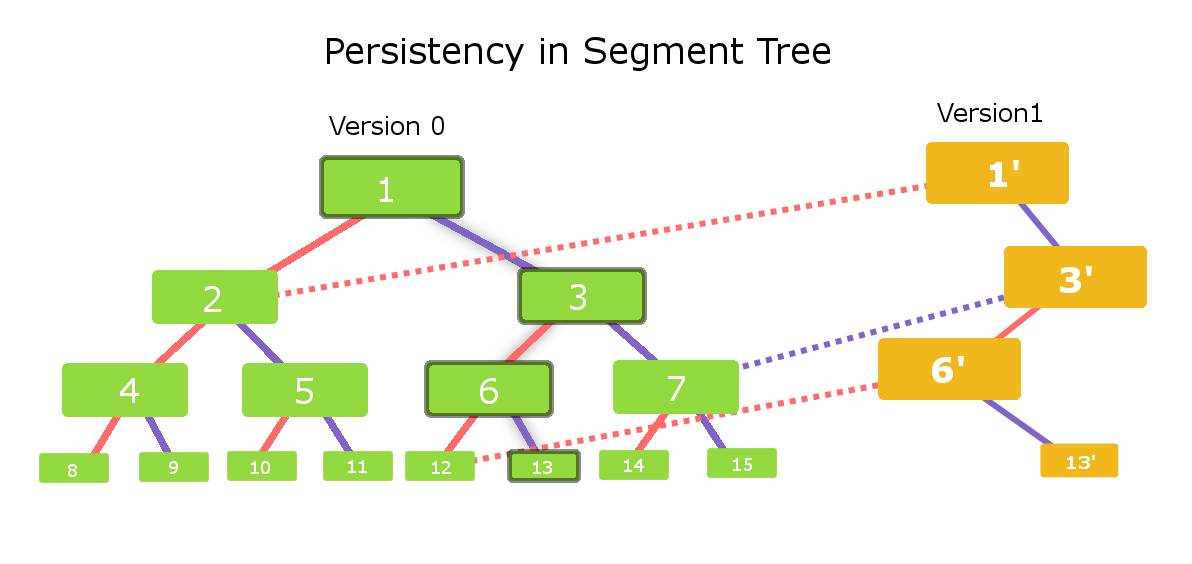

Код для ДО сверху

Тут все просто, копируете вручную лист, который изменился, а дальше поднимаетесь по дереву вверх и, используя конструктор st_node, создаете новые вершины.