!Мастер-теорема

Эта теорема позволяет оценить сверху асимптотику работы любого алгоритма, который использует идею разделяй и властвуй.

Определение

Все алгоритмы, использующие идею разделяй и властвуй, делят одну задачу размера n на a задач, которые в b раз меньше исходной, а потом объединяют все это за $\Theta (n^c)$. Тогда их можно записать с помощью данной рекурренты:

aT(\frac{n}{b}) + \Theta(n^c), & n > n_{0}\\ \Theta(1), & n \leq n_{0} \end{cases}

где у нас есть решение для задач размера меньше $n_0$ за $\Theta (1)$.

Это дерево рекурсии алгоритма при а = 2.

В общем теорема говорит: 1. При $c>{\log }_{b}a$, $T(n)=\Theta (n^c)$ 2. При $c={\log }_{b}a$, $T(n)=\Theta (n^c{\log }_{b}n)$ 3. При $c<{\log }_{b}a$, $T(n)=\Theta (n^{{\log }_{b}a})$

Математическое доказательство

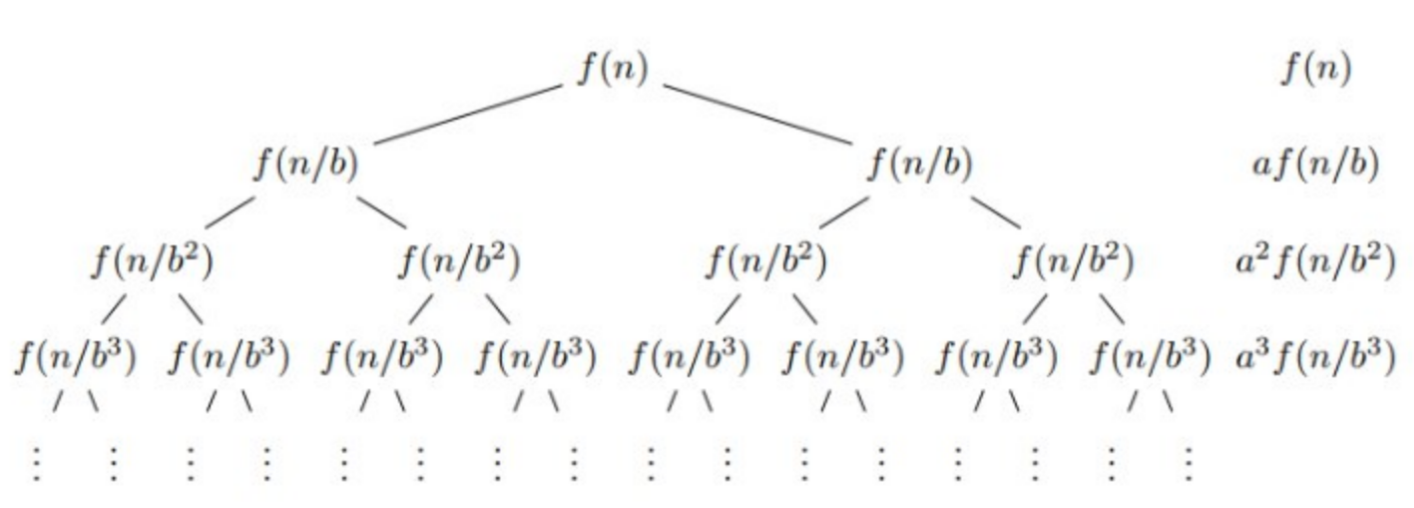
Разберем 3 варианта: 1. $c>{\log }_{b}a$ 2.$c={\log }_{b}a$ 3.$c<{\log }_{b}a$ Рассмотрим дерево рекурсии, а точнее отдельный $k-ый$ уровень в нем. На нем $a^k$ вершин, который являются задачами размера $\frac{n}{b^k}$ и обобщаются до предыдущего уровня за $(\frac{n}{b^k}{)}^c$. Уровней у нас всего ${\log }_{b}n$, если просуммировать по ним, используя эту формулу, то мы получим общую сложность: $T(n)={\sum }_{k=0}^{{\log }_{b}n}{a}^k{\left(\frac{n}{b^k}\right)}^c=n^c{\sum }_{k=0}^{{\log }_{b}n}{\left(\frac{a}{b^c}\right)}^k$ Теперь становится понятно разделение на 3 варианта, в первом у нас получатся сумма убывающей геометрической прогрессии, которая ограничена сверху константой, а значит общая сложность будет равна $\Theta (n^c)$. Во втором случае у нас получается формула: $T(n)=n^c{\sum }_{k=0}^{{\log }_{b}n}{1}^k=n^c{\log }_{b}n$ А значит все будет работать за $\Theta (n^c{\log }_{b}n)$ В третьем же случае у нас сумма возрастающей геометрической прогрессии, которая асимптотически равна своему старшему члену, а значит: $T(n)=\Theta \left(n^c{\left(\frac{a}{b^c}\right)}^{{\log }_{b}n}\right)=\Theta \left(\frac{n^c\ast a^{{\log }_{b}n}}{n^c}\right)=\Theta (a^{{\log }_{b}n})=\Theta (n^{{\log }_{b}a})$

В этом случае итоговая сложность алгоритма выйдет $\Theta (n^{{\log }_{b}a})$.

Примеры

Рассмотрим сортировку слиянием. В ней a = 2, b = 2, а c = 1, а значит асимптотика работы этого алгоритма равна $\Theta (n{\log }_{2}n)$.