!Полиномиальное хеширование

Краткое описание

Хеширование - базовый алгоритм для сравнения строк за $O(1)$ с предподсчетом за $O(n)$ вместо тупого поэлементного сравнения за $O(n)$. Бывает полезно если в задаче вы работаете со строками, суммарная длина которых не очень велика¹, но с которыми нужно провести много сравнений.

Идея алгоритма

Идея хеширования заключается в том, что сравнение чисел происходит быстрее, чем сравнение других объектов, и если придумать алгоритм, который сможет преобразовать строчку в число и сравнить получившиеся числа, которым хеширование и является, то сравнение будет происходить за $O(1)$. Важные свойства хеширования: 1. Из одинаковых объектов получаются одинаковые числа 2. При небольшом изменении исходного объекта его хеш должен сильно меняться.

Описание алгоритма

Для работы этого алгоритма нужно выбрать 2 простых числа, один из них будет модулем - MOD, другой основанием - P. Пусть длина нашей строки - n, тогда весь наш хеш будет храниться в массиве длиной n+1, ведь удобнее использовать 0-нумерацию. Нулевая ячейка пустая, в $i+1ой$ ячейки массива hash будет лежать: $s_0\ast P^0+s_1\ast P^1+\cdots +a_{i-1}\ast P^{i-1}+a_i\ast P^i\mathrm{mod}MOD$. Это хеширование называется прямым, есть также и обратное, формула $i+1ой$ ячейки в нем выглядит так: $s_0\ast P^i+s_1\ast P^{i-1}\dots s_{i-1}\ast P^1+s_i\ast P^0$Тогда, чтобы получить хеш любого полуинтервала с $l$ по $r$ за $O(1)$, нам надо взять это $\frac{hash[r]-hash[l]}{P^l}\mathrm{mod}MOD$ для прямого хеширования и $(hash[r]-hash[l]\ast P^r)\mathrm{mod}MOD$ для обратного. Чтобы не считать каждую ячейку отдельно, можно пересчитывать их через предыдущие, для прямого хеширования можно воспользоваться формулой: $hash[i]=hash[i-1]+s_i\ast P^i$ для обратного: $hash[i]=hash[i-1]\ast P+s_i$ что намного удобнее пишется и вычислять хеш подстроки также удобнее, потому что не нужно писать быстрое возведение в степень из-за которого возникает дополнительный $lo{g}_2(n)$ при каждом взятии хеша. Так что обратный полиномиальный хеш лучше, чем прямой, но если вам удобнее писать прямой, то пишите его.

Проблемы хеширования

Хеширование гарантирует, что одинаковые строки будут иметь одинаковый хеш, но не гарантирует того, что разные строки имеют разный хеш. Более того, этот факт нельзя гарантировать, ведь если честно нумеровать строки так, чтобы это выполнялось, то даже для достаточно небольших строк у нас возникнет переполнение. Потому что если алфавит имеет размер M, а длина строки максимум L, то для хранение отдельного идентификатора для всех возможных строк нам нужно $M^L$ возможных цифровых значений строки, если мы будем использовать латинский алфавит, то нам получится записать всего 13 символов. Поэтому в алгоритме используется взятие по модулю, которое создает вероятность того, что разные строки будут иметь одинаковый хеш, что называется коллизиями. Избежать их невозможно, но некоторые параметры влияют на их частоту, так, например, модуль и основание являются взаимно простыми числами как раз для того, чтобы при изменении небольшого количества символов вероятность коллизии была мала. Важно, чтобы основание было больше номера максимально элемента алфавита, ведь иначе получить коллизию очень просто, это легко понять, если сравнить хеширование с системой счисления, если максимальное число, хранящееся в одном бите больше, чем минимальное число, хранящееся в следующем, то к одному и тому же числу будет несколько разных записей, различающихся только в этих двух битах. Также сам алгоритм построен так, чтобы элементы на разных позициях, при изменении, разительно влияли на итоговый хеш. Если вы переживаете, что задача не заходит из-за коллизий напишите двойное хеширование, которое считает второй хеш по другому модулю и с другим основанием, чтобы вероятность коллизии стала катастрофически мала.

Хеширование со взломами

Если вы пишете раунд на популярном сайте для программирования Codeforces, или других олимпиадах, поддерживающих взломы, то хеширование может быть взломано и чтобы этого избежать, можно попробовать использовать двойное хеширование, но при достаточном усердии его тоже можно взломать. И чтобы такого не произошло, второе хеширование надо сделать по рандомному основанию, что приводит к низкой вероятности коллизии, из-за хеширования по простому основанию, но к невозможности взлома из-за рандомного основания. Главное, использовать рандом, который не взламывается на Codeforces.

Хеширование других объектов

Хеширование других объектов используется для проверки на изоморфизм.

Множества

Множества не содержат одинаковых элементов, что позволяет нам посчитать хеш от них всех и проксорить, и так как одинаковых элементов нет, то проблемы не возникнет и все это будет работать за $O(n)$.

Игры

Игры также можно хешировать, но чтобы это делать было проще, можно сложную позицию разбить на много маленьких, после чего приписать число каждой и проксорить их между собой. Например в шахматах и шашках есть поля, если для каждого состояния каждого поля придумать свое рандомное значение, которое отвечает за то, что там стоит, то их xor и будет состоянием игры, которое также можно легко пересчитать при небольшом изменении игры, например ходе одного из игроков.

Подматрицы

С помощью хеширования можно также сравнивать подматрицы за $O(1)$ по времени. Для этого можно завести два основания $P_h$ - основание по горизонтали и $P_v$ - основание по вертикали. Насчитаем хеш для всех ячеек по формуле: $hash[i][j]=hash[i-1][j]+hash[i][j-1]-hash[i-1][j-1]+A[i][j]\ast P_h^i\ast P_u^j$ Таким образом, чтобы посчитать хеш на подматрице $A_{x_1:x_2,y_1:y_2}$ нам всего лишь нужно посчитать выражение: $(hash[x_2][y_2]-hash[x_1-1][y_2]-hash[x_2][y_1-1]+hash[x_1-1][y_1-1])\ast P_h^{n-x_1}\ast P_u^{m-y_1}$

Деревья

Чтобы проверить два дерева на изоморфизм, нам придется честно рекурсивно считать хеш функцию от детей вершины, потом пересчитывая хеш самой вершины от упорядоченного массива хешей ее детей. Полиномиальный хеш использовать нельзя, ведь есть простейшие примеры, в которых хеши разных деревьев совпадают: 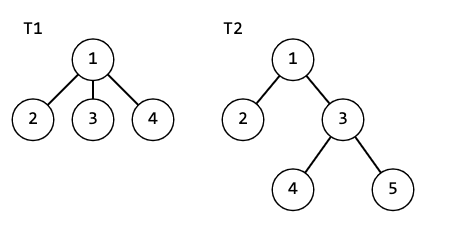Так что надо использовать какую-то функцию заместо. Подойдет такая: $h(u)=239+\Sigma \log (h(v))$ где $v$ - сын $u$ в дереве. Сортировать массив детей обязательно, ведь иначе из-за погрешности может не сойтись хеш одинаковых объектов. Получается сложность $O(n\ast lo{g}_{2}n)$. Если корень вам не дан, то найдите центроид и запускайтесь от него, как от корня. Если их несколько, то можно посчитать хеш для обоих, если они были бы корнями и взять минимум из этих двух значений.

Примеры

Вот класс, реализующий двойное обратное хеширование, в котором второе основание - рандомное число:

random_device r_d;
mt19937 rnd(r_d());
 
long long rnd_hash_base = rnd() % 500 + 240;
 
struct Hash {
	long long MOD1 = 2286661337, base1 = 239, MOD2 = 1000000007,
	base2 = rnd_hash_base;
	vector<long long> hash1, hash2, deg1, deg2;
	Hash(string s) {
		hash1.resize(s.size() + 1);
		hash2.resize(s.size() + 1);
		deg1.resize(s.size());
		deg2.resize(s.size());
		deg1[0] = 1;
		deg2[0] = 1;
		for (long long i = 1; i < deg1.size(); i++) {
			deg1[i] = (deg1[i - 1] * base1) % MOD1;
			deg2[i] = (deg2[i - 1] * base2) % MOD2;
		}
		long long mn = MOD1;
		for (auto i : s) {
			mn = min(mn, (long long)(i - 1));
		}
		for (long long i = 0; i < s.size(); i++) {
			hash1[i + 1] = (hash1[i] * base1 + s[i] - mn) % MOD1;
			hash2[i + 1] = (hash2[i] * base2 + s[i] - mn) % MOD2;
		}
	}
	pair<long long, long long> get_hash(long long l, long long r) {
		auto ans1 = (MOD1 + hash1[r] - (hash1[l] * deg1[r - l]) % MOD1) % MOD1;
		auto ans2 = (MOD2 + hash2[r] - (hash2[l] * deg2[r - l]) % MOD2) % MOD2;
		return {ans1, ans2};
	}
	bool compare(Hash &Hash1, long long l1, long long r1, long long l2,
	long long r2) {
		if (r1 - l1 != r2 - l2) {
			return false;
		}
		auto res1 = get_hash(l1, r1);
		auto res2 = Hash1.get_hash(l2, r2);
		return res1.first == res2.first && res1.second == res2.second;
	}
};

Footnotes

1. Не превышает $10^8$ в худшем случае, идеально, если ограничено $10^6$ ↩